Russell’s Paradox: a historical study about the paradox in Frege’s theories
DOI:
10.47976/RBHM2018v18n351-22Palavras-chave:
Mathematic, History, Russell‟s Paradox, Gottlob FregeResumo
For over twenty years, Frege tried to find the foundations of arithmetic through logic, and by doing this, he attempted to establish the truth and certainty of the knowledge. However, when he believed his work wasdone, Bertrand Russell sent him a letter pointing out a paradox, known as Russell‟s paradox. It is often considered that Russell identified the paradox in Frege‟s theories. However, as shown in this paper, Russell, Frege and also George Cantor contributedsignificantly to the identification of the paradox. In 1902, Russell encouraged Frege to reconsider a portion of his work based in a paradox built from Cantor‟s theories. Previously, in 1885, Cantor had warned Frege about taking extensions of concepts in the construction of his system. With these considerations, Frege managed to identify the precise law and definitions that allowed the generation of the paradox in his system. The objective of this paper is to present a historical reconstruction of the paradox in Frege‟s publications and discuss it considering the correspondences exchanged between him and Russell. We shall take special attention to the role played by each of these mathematicians in the identification of the paradox and its developments. We also will show how Frege anticipated the solutions and new theories that would arise when dealing with logico-mathematical paradoxes, including but not limited to Russell‟s paradox.
Downloads
Métricas
Referências
ASSIS NETO, F.R. 2008. Prefácio ao Begriffschrift de Gottlob Frege (1848-1925): tradução e introdução ao texto.In:Revista Brasileira de História da Matemática, vol. 8,n.16.123-141.
BACHA, M.L.;SAITO, F. 2014. Peirce e Cantor: um estudo preliminar sobre continuidade e infinitesimais.In:Revista Brasileira de História da Matemática.vol. 14, n.28.1-23.
BEANEY, M.2005. Frege, Russell and logicism.In:Gottlob Frege: Critical assessments of leading philosophers (pp. 213-233).New York: Routledge.
BURGESS, J. P. 2005. Fixing Frege.New Jersey: Princeton University Press.
COURY, A. G. F. 2015. Frege e as leis da aritmética: do ideal de fundamentação ao paradoxo. Dissertação (Mestrado). Universidade Federal de São Carlos.
DA SILVA, J.J. 2003. O Segundo Problema de Hilbert.In:Revista Brasileira de História da Matemática. vol. 3, n.5.29-37.
DAVIS, P.J. & HERSH, R. 1981. The Mathematical Experience.Boston: Mariner Books.
D‟OTTAVIANO, I. M. L. 1990. Paradoxos auto-referenciais e as lógicas não clássicas heterodoxas.In:Ciência e Cultura.vol. 42, n. 2.164-123.
DUMMET, M. 1991. Frege: Philosophy of Mathematics. London: Duckworth.
FRAENKEL, A.A., BAR-HILLEL, Y., LEVY, A. 1984. Foundations of Set Theory.Holanda: Elsevier Science Publishing Company.
FREGE, G.1970. Begriffsschrift: a formula language, modeled upon that of arithmetic, for pure thought. In:J. van Heijenoort (Ed. and Trans.) Frege and Gödel: two fundamental texts in mathematical logic. Cambridge, Massachusetts: Harvard University Press.
Downloads
Publicado
Métricas
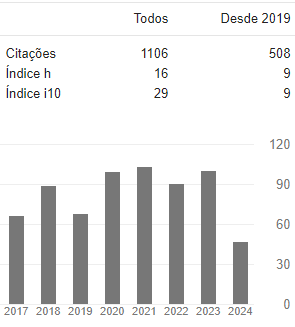
Visualizações do artigo: 409 PDF downloads: 305