THE LINEAR INDETERMINATE EQUATION - A BRIEF HISTORICAL ACCOUNT
DOI:
10.47976/RBHM2015v15n3083-94Palavras-chave:
Indeterminate equation, Chinese remainder theorem, Aryabhata, Kuttaka, Brahmagupta, BhaskaraResumo
The paper presents in brief the contribution of Aryabhata in developing general solution of indeterminate equation of the type ax + c = by, where a, b, c are the integers. Also the contributions of Bhaskara and Brahmagupta in developing the solution of the indeterminate equations are discussed. Finally an example of Paramesvara is illustrated to solve coupled linear indeterminate equations which may be adopted to find the multiplicative inverse in a group that is of interest in cryptology, signal processing, coding and computer design.
Downloads
Não há dados estatísticos.
Métricas
Carregando Métricas ...
Referências
AYANGAR, A.A. K, 1926, The Mathematics of Aryabhata, Quarterly Journal of Mythic Society, Vol.16, pp 158-179.
BAG, A. K., 1977, The method of Integral Solution of Indeterminate Equations of the type by=ax +/- c in Ancient Medieval India, Indian Journal of History of Science, Vol.12, pp. 1-16.
CLARK, W. E., 1930, The Aryabhatiya of Aryabhata : Translation with notes, The University of Chicago Press, Chicago, Illinois.
DATTA, B. and Singh, A. N. ,1962, History of Hindu Mathematics, a source book, Parts 1 and 2, Asia Publishing House, Bombay.
Elements of Euclid (Translation and commentaries by Heath, Thomas, L.), Dover Publications, 1956.
HANG, Chin-Chen and YANG, Jen –Ho, 2009, A parallel algorithm base don Aryabhatta remainder Theorem for Residue number System, International Journal of Innovative Computing, Information and Control, Vol. 5(7), pp. 2053 - 2060.
BAG, A. K., 1977, The method of Integral Solution of Indeterminate Equations of the type by=ax +/- c in Ancient Medieval India, Indian Journal of History of Science, Vol.12, pp. 1-16.
CLARK, W. E., 1930, The Aryabhatiya of Aryabhata : Translation with notes, The University of Chicago Press, Chicago, Illinois.
DATTA, B. and Singh, A. N. ,1962, History of Hindu Mathematics, a source book, Parts 1 and 2, Asia Publishing House, Bombay.
Elements of Euclid (Translation and commentaries by Heath, Thomas, L.), Dover Publications, 1956.
HANG, Chin-Chen and YANG, Jen –Ho, 2009, A parallel algorithm base don Aryabhatta remainder Theorem for Residue number System, International Journal of Innovative Computing, Information and Control, Vol. 5(7), pp. 2053 - 2060.
Downloads
Publicado
30-10-2020
Métricas
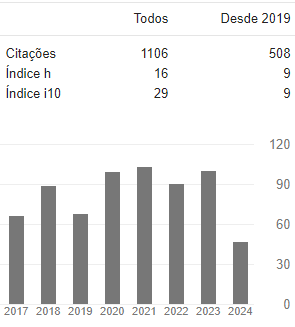
Visualizações do artigo: 285 PDF downloads: 210
Como Citar
SHUKLA, Kedar N. THE LINEAR INDETERMINATE EQUATION - A BRIEF HISTORICAL ACCOUNT. Revista Brasileira de História da Matemática, São Paulo, v. 15, n. 30, p. 83–94, 2020. DOI: 10.47976/RBHM2015v15n3083-94. Disponível em: https://rbhm.org.br/index.php/RBHM/article/view/86. Acesso em: 3 jun. 2025.
Edição
Seção
Artigos