Mr. Bayes and the classics: a suggested interpretation
DOI:
10.47976/RBHM2022v22n4301-16Palabras clave:
law of large numbers, inverse probability, De Moivre, Thomas Bayes, Bayesian inferenceResumen
The main hypothesis about Thomas Bayes’s intentions to write his famous {\it Essay} on probability is that he wanted to refute the arguments of David Hume against the reliability of the occurrence of miracles, published in 1748. In this paper we argue that it was not Bayes’s intention to rebut Hume but that his interest on the ``inverse problem'' came about as result of his study of the second edition of Abraham De Moivre’s book, {\it The Doctrine of Chances}, published in 1738. A possible communication of Bayes’s breakthrough might have annoyed De Moivre, leading to a response written for Bayes in the third edition of De Moivre’s book, published in 1756. Among other points, the response claims that De Moivre was the first to solve the mentioned inverse problem. Under this perspective Richard Price’s letter, written as preface to Bayes’s essay, has a new interpretation, appearing also as a defense of Bayes premiership on a satisfactory or proper solution.
Descargas
Métricas
Citas
Allen, R. C. (1999). David Hartley on Human Nature. State University of New York Press, Albany. Bayes, T. (1731). Divine Benevolence: Or, An Attempt to Prove that the Principal End of the Divine
Providence and Government is the Happiness of His Creatures. John Noon, London.
Bayes, T. (1736). An Introduction to the Doctrine of Fluxions, and Defence of the Mathematicians against the Objections of the Author of the Analyst, so far as they are designed to affect their general Methods of Reasoning. John Noon, London.
Bayes, T. (1763a). An Essay Towards Solving a Problem in the Doctrine of Chances. Philosophical Transactions of the Royal Society, 53:370–418.
Bayes, T. (1763b). A letter from the late Reverend Mr. Thomas Bayes, F.R.S. to John Canton, M.A. & F.R.S. Philosophical Transactions of the Royal Society, 53:269–271.
Bellhouse, D. R. (2002). On some Recently Discovered Manuscripts of Thomas Bayes. Historia Mathe- matica, 29:383–394.
Bellhouse, D. R. (2004). The Reverend Thomas Bayes, F.R.S.:a biography to celebrate the tercentenary of his birth. Statistical Science, 19:3–43.
Bellhouse, D. R. (2007). Lord Stanhope’s papers on the Doctrine of Chances. Historia Mathematica, 34:173–186.
Bellhouse, D. R. (2010). The pure mathematics curriculum in the English dissenting academies. Unpub- lished manuscript.
Bellhouse, D. R. (2011). Abraham De Moivre. Setting the stage for classical probability and its applications. CRC Press, Boca Raton.
Bernoulli, J. (1713). Ars Conjectandi. Thurneysen brothers, Basel.
Bernoulli, J. (2006). The art of conjecturing, together with Letter to a friend on sets in court tennis; translated with an introduction and notes by Edith Dudley Sylla. The John Hopkins University Press, Baltimore.
Dale, A. I. (1986). A newly-discovered result of Thomas Bayes. Archive for History of Exact Sciences, 35:101–113.
Dale, A. I. (1988). On Bayes’ theorem and the inverse Bernoulli theorem. Historia Mathematica, 15:348– 360.
Dale, A. I. (2003). Most Honourable Remembrance. The Life and Work of Thomas Bayes. Springer, New York.
Daston, L. (1988). Classical Probability in the Enlightenment. Princeton University Press, Princeton.
De Moivre, A. (1730). Miscellanea Analytica de Seriebus et Quadraturis. J. Tonson and J. Watts, London.
De Moivre, A. (1738). The Doctrine of Chances: or, A Method of Calculating the Probabilities of Events in Play. H. Woodfall, London.
De Moivre, A. (1756). The Doctrine of Chances: or, A Method of Calculating the Probabilities of Events in Play. A. Millar, London.
De Morgan, A. (1860). Rev. Thomas Bayes, etc. Notes and Queries, 9:9–10.
Doddridge, P. (1763). A Course of Lectures, on the principal subjects in Pneumatology, Ethics and Divinity. Buckland et al., London.
Edwards, A. W. F. (1986). Is the reference to Hartley (1749) to Bayesian inference? The American Statistician, 40:109–110.
Gorroochurn, P. (2012). Classic problems of probability. Wiley, New Jersey.
Hacking, I. (1971). Jacques Bernoulli’s Art of Conjecturing. British Journal for the Philosophy of Science, 22:209–229.
Hacking, I. (1975). The Emergence of Probability. Cambridge University Press, Cambridge.
Hacking, I. (1990). The Taming of Chance. Cambridge University Press, Cambridge.
Halley, E. (1693). An estimate on the degrees of mortality of mankind, drawn from curious tables of the birth and funerals at the city of breslaw; with an attempt to ascertain the price of annuities upon lives. Philosophical Transactions of the Royal Society, 17:596–610.
Hartley, D. (1733). Reasons Why the Practice of Inoculation Ought to be introduced into the Town of Bury at Present. Bury St. Edmunds.
Hartley, D. (1749). Observations on man, his frame, his duty, and his expectations. J. Leake, W. Frederick, C. Hitch & S. Austen, London.
Haydon, C. (2009). Maddox, Isaac (1697–1759), bishop of Worcester.
Hume, D. (1739). A Treatise of Human Nature. John Noon (vols. 1 & 2) and Thomas Longman (vol. 3, 1740), London.
Hume, D. (1740). An Abstract of a book lately published; entituled, A Treatise of Human Nature, &c. C. Borbet, London.
Hume, D. (1748). Philosophical Essays concerning Human Understanding. A. Millar, London.
Hume, D. (1779). Dialogues concerning Natural Religion. London.
Hume, D. (2000). An Enquiry Concerning Human Understanding. Edited by Tom L. Beauchamp. Clarendon Press, Oxford.
Laplace, P.-S. (1774). M ́emoire sur la probabilit ́e des causes par les ́ev ́enements. M ́emoire de l’Acad ́emie Royale des Sciences de Paris (savants ́etrangers), 6:621–656.
Maclaurin, C. (1748). An Account of Sir Isaac Newton’s Philosophical Discoveries. London.
Maddox, I. (1750). The Expediency of preventive Wisdom. H. Whitridge, London.
Norton, D. F. and Norton, M. J. (1996). The David Hume Library. Edinburgh Bibliographical Society.
Price, R. (1758). A Review of the Principal Questions and Difficulties in Morals. A. Millar, London.
Price, R. (1764). A Demonstration of the Second Rule in the Essay toward the Solution of a Problem in the Doctrine of Chances. Philosophical Transactions of the Royal Society, 54:296–325.
Singer, B. (1979). Distribution-free methods for non-parametric problems: A classified and selected bibli- ography. British Journal of Mathematical and Statistical Psychology, 32:1–60.
Stigler, S. M. (1983). Who discovered Bayes’s theorem? The American Statistician, 37:290–296. Stigler, S. M. (2013). The True Title of Bayes’s Essay. Statistical Science, 28:283–288. Todhunter, I. (1865). A History of Mathematical Probability. Macmillan, Cambridge.
Walker, H. (1934). Abraham De Moivre. Scripta Mathematica, 2:316–333.
Webb, M. E. (1988). A new history of Hartley’s Observations on Man. Journal of the History of the Behavioral Sciences, 24:202–211.
Descargas
Publicado
Métricas
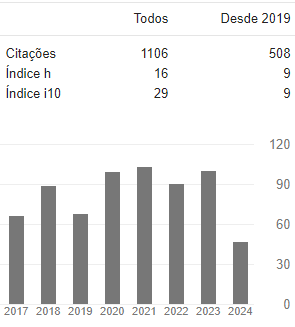
Visualizações do artigo: 449 PDF (Português (Brasil)) downloads: 313