Russell's Paradox: A Historical Study about the Paradox in Frege's Theories
DOI:
10.47976/RBHM2019v19n3795-116Keywords:
Mathematics, History, Russell’s Paradox, Gottlob FregeAbstract
For over twenty years, Frege tried to find the foundations of arithmetic through logic, and by doing this, he attempted to establish the truth and certainty of the knowledge. However, when he believed his work was done, Bertrand Russell sent him a letter pointing out a paradox, known as Russell’s paradox. It is often considered that Russell identified the paradox in Frege’s theories. However, as shown in this paper, Russell, Frege and also George Cantor contributed significantly to the identification of the paradox. In 1902, Russell encouraged Frege to reconsider a portion of his work based in a paradox built from Cantor’s theories. Previously, in 1885, Cantor had warned Frege about taking extensions of concepts in the construction of his system. With these considerations, Frege managed to identify the precise law and definitions that allowed the generation of the paradox in his system. The objective of this paper is to present a historical reconstruction of the paradox in Frege’s publications and discuss it considering the correspondences exchanged between him and Russell. We shall take special attention to the role played by each of these mathematicians in the identification of the paradox and its developments. We also will show how Frege anticipated the solutions and new theories that would arise when dealing with logico-mathematical paradoxes, including but not limited to Russell’s paradox.
Downloads
Metrics
References
FURTH, M. 1964. Introduction. In M. Furth (Ed.) The Basic Laws of Arithmetic: exposition of the system. Berkeley, Los Angeles: University of California Press.
GOLDSTEIN, R. 2008. Incompletude: a prova e o paradoxo de Kurt Gödel. I. Korytowski (Trans.) São Paulo: Companhia das Letras.
Downloads
Published
Métricas
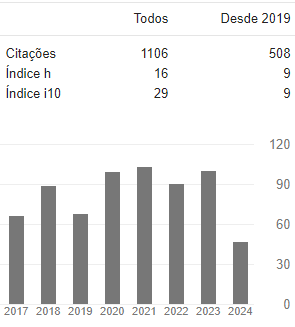
Visualizações do artigo: 460 PDF (Português (Brasil)) downloads: 278